学習目標
- 相関係数が変数間の関係を示すことを説明できる。
- 相関関係は、変数間の因果関係を示すものではないことを認識する。
- 実際には存在しない変数間の関係を探してしまう傾向があることを説明する。
- 無作為抽出と、実験群と対照群への参加者の割り当てについて説明する。
- 実験者や参加者の偏りが実験結果にどのように影響するかを説明できる
- 独立変数と従属変数を識別する
アイスクリームの売り上げが増えると、犯罪の発生率も増えることをご存知ですか?
好きな味のアイスクリームを堪能することで、犯罪に走る可能性があるのでしょうか?
あるいは、犯罪を犯した後に、自分へのご褒美としてコーンを食べようと思うのでしょうか?
アイスクリームと犯罪の間に関係があることは疑いの余地がありませんが(例:Harper, 2013)、一方が他方の発生を実際に引き起こした、と判断するのはかなり愚かなことです。
アイスクリームの売り上げも犯罪率も、外の気温に関係している可能性の方がはるかに高いといえます。気温が高ければ、たくさんの人が家から出て、お互いに交流し、お互いに迷惑をかけ、時には犯罪を犯すこともあるでしょう。また、外が暖かいと、アイスクリームのような冷たいものを求める傾向があります。
二つのものの間に本当に関係があるかどうかは、どのように判断するのでしょうか?また、関係がある場合、それが偶然なのか、それとも因果関係なのかをどのように見極めればよいのでしょうか?
相関研究
相関関係とは、2つ以上の変数(アイスクリームの消費量と犯罪など)の間に関係があることを意味しますが、この関係は必ずしも原因と結果を意味するものではありません。2つの変数に相関があるということは、一方の変数が変化すると、もう一方の変数も変化するということです。相関関係を測定するには、相関係数という統計値を算出します。相関係数とは、変数間の関係の強さと方向性を示す-1から+1までの数値のことです。相関係数は通常、rという文字で表されます。
相関係数の数字の部分は、関係の強さを示しています。数字が1に近ければ近いほど(それが負であれ正であれ)、変数はより強く関連しており、一方の変数の変化が他方の変数の変化に伴ってより予測可能であることを意味します。数字が0に近いほど、関係が弱く、変数間の関係が予測できなくなります。例えば、相関係数が0.9の場合、相関係数が0.3の場合よりもはるかに強い関係を示します。アイスクリームと犯罪に関する上記の例は、お互いに関係がないと思われる2つの変数の例です。
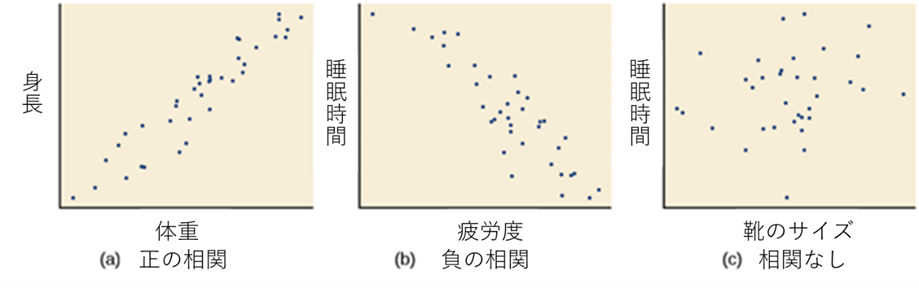
相関係数の符号(正または負)は、関係の方向性を示します(図2.12)。正の相関は、変数が同じ方向に動いていることを意味します。別の言い方をすれば、一方の変数が増加すると他方の変数も増加し、逆に一方の変数が減少すると他方の変数も減少するということを意味します。負の相関とは、変数が反対方向に動くことを意味します。2つの変数が負の相関関係にある場合、一方の変数の減少は他方の変数の増加を伴い、その逆もまた然りです。
アイスクリームと犯罪率の例は、気温が高くなると両方の変数が増加するため、正の相関関係にあります。その他の正の相関関係の例としては、個人の身長と体重の関係や、人の年齢とシワの数の関係などがあります。また、日中の疲労感と前日の睡眠時間には負の相関があると考えられます。
負の相関の実例として、ミネソタ大学の学生研究者は、睡眠時間が5時間未満であった週の平均日数とGPAの間に弱い負の相関(r = -0.29)があることを発見しました(Lowry, Dean, & Manders, 2010)。負の相関があることは、相関がないということとは異なるということに注意してください。例えば、睡眠時間と靴のサイズには相関がないと考えられます。
先に述べたように、相関関係には予測価値があります。あなたが主要大学の入学審査委員だと想像してみてください。膨大な数の出願書類に直面していますが、入学を許可できるのは出願者のほんの一部に過ぎません。では、どのようにして入学者を決定するのでしょうか。現在の学生の大学でのGPAと、SATやACTなどの標準化テストのスコアとの相関関係を調べてみましょう。現在の学生のどの相関が最も強いかを観察することで、この情報を利用して、大学に入学を申請した学生の相対的な成功を予測することができます。
学習へのリンク
このインタラクティブな散布図を操作して、正負の相関関係の理解を深めてください。





